Mathematik

Im Rahmen meiner Doktorarbeit (Approximation of some nonlocal operators in a sinc-basis, 2024), habe ich mich mit numerischen Verfahren für nichtlokale partielle Differentialgleichungen beschäftigt.

Ein prototypisches Beispiel für so eine Gleichung ist das fraktionale Dirichlet Problem: finde \(u\) so dass

\((-\Delta)^s u = f \text{ in }\Omega, u = 0 \text{ in }\mathbb R^d \setminus\Omega.\)

Dabei ist \((-\Delta)^s\) der fraktionale Laplace Operator in der Integraldefinition, nämlich

\((-\Delta)^s u(x) = C(d,s) \int_{\mathbb R^d} \frac{u(x) – u(y)}{|x-y|^{d+2s}} \mathrm d y.\)

Diese Definition stellt den nichtlokalen Charakter des Operators heraus: um \((-\Delta)^s u(x)\) an einem Punkt \(x\) auszurechnen muss ein Integral über den ganzen \(\mathbb R^d\) ausgerechnet werden. Dies bringt Schwierigkeiten bei der numerischen Behandlung solcher Probleme mit sich.

Gleichzeitig lassen sich solche nichtlokalen Modelle anwenden, um Phänomene zu modellieren und vorherzusagen. Beispiele dafür sind das Jagdverhalten von Tieren oder die Verbreitung von Pandemien über dem Globus.

Der fraktionale Laplace Operator kann auf \(\mathbb R^d\) äquivalent als Fourier Symbol \( |\omega|^{2s}\) definiert werden in dem Sinne das

\(\mathcal F (-\Delta)^s u = |\omega|^{2s} \mathcal F u\)

gilt. Dies habe ich in meiner Doktorarbeit genutzt, um ein numerisches Verfahren basieren auf sinc-Funktionen zu entwickeln, mit dem Probleme wie das obige effizient gelöst werden können. Grundlage dafür ist, dass die sinc-Funktion eine Fourier Transformation hat, die die Indikatorfunktion eines (Hyper)-Würfels ist.

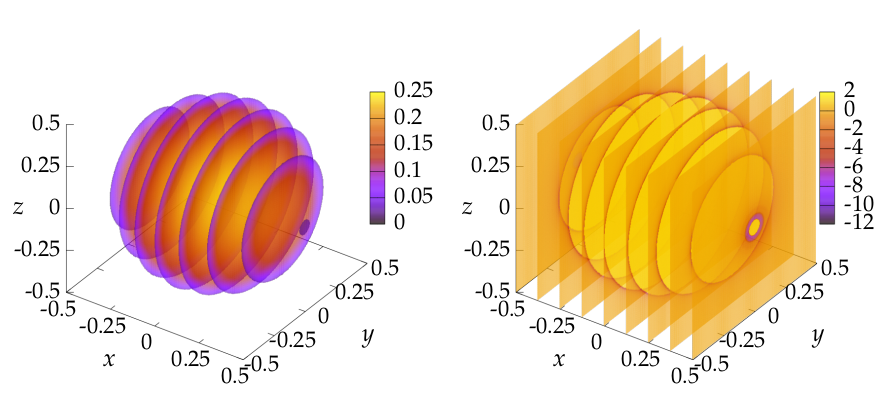
Exemplarisch zeigt das folgende Bild die mit diesem Verfahren berechnete, näherungsweise Lösung $u_h$ zum fraktionalen Dirichlet Problem mit \(f = 1\) auf dem dreidimensionalen Ball (links) sowie \((-\Delta)^s u_h\) (rechts).